信号处理领域的利器-压缩感知

随着信息量的增加，数据采集、传输和存储设备面临着越来越严重的压力；数据处理也伴随着信息泄露的风险，部分数据丢失可能威胁到生命和财产的安全，现在数据泄露并不少见。因此，在大数据时代，人们迫切需要找到一种新的数据处理 *** 来降低信息处理过程中的数据泄存、传感器等硬件设备的压力。

压缩感知理论是在这种背景下产生的一种新兴的信号采集和编解码理论。该理论指出，无论是什么类型的信号，在原始域或某些变换域中总是稀疏或可压缩在传输过程中远低于传统奈奎斯特采样的线性投影值，实现信号的准确性或高概率重建。

这一理论带来了信号采样理论的变化，对信息安全也具有重要意义。学者将压缩感知应用于图像加密密和传输、信息的安全编码技术、信息的安全存储和无线传感器 *** 的数据采集。许多信息处理和信息安全领域的学者对压缩感知有着浓厚的研究兴趣。本文首先简要介绍了压缩感知的诞生，然后简要介绍了理论内容和一些应用 *** ，并结合实际情况讨论了一些成功的应用。

一.压缩感知的起源

“压缩感知”思想最早出现在一篇2000年左右的博士论文中《Near-Optimal Signal Recovery From Random Projections》[1]中间。当时加州理工学院教授的发现可以说是一场意外。Emmanuel Candès在研究名叫Shepp-Logan Phantom计算机科学家和工程师经常用这种标准图像来测试图像还原算法。检查的图像质量很差，充满噪音，他用了L-1范数最小化的数学算法去除噪声条纹，结果算法真的起作用。这个算法是一个NP难题转化为凸优化问题，充分体现了压缩感知的思想:通过优化算法高概率还原信号(如图1所示)。“就像前三个给出10个银行卡账户一样，我可以猜到后七个，而且，反复尝试。”这是压缩感知思想的开始。

图1 加入各种噪声后的图像还原图

后来，Candès在与陶哲轩的交流中，陶哲轩也开始思考这个问题，上述交流已成为压缩感知论文的基础。另一位奠基人是Donoho，他的代表作《Compressed sensing》[2]可以说是一篇完整系统地阐述压缩感知原理和推导的论文。

这些都是压缩感知的起源。

二.压缩感知理论内容及获取和解决方案

压缩感知理论本身的含义是“高精度重建[3]”，在理论框架下，采样速率不再取决于信号的带宽，而是取决于稀疏性和非相关性两个基本标准。

压缩感知理论

主要包括三部分：

(1)信号稀疏表示；

(2)设计测量矩阵，确保原始信号同时降低维数x的信息损失最小;

(3)使用设计信号恢复算法M个别观测值无失真恢复长度N原始信号。

理论依据[4]Candès推导和证明)

(1)设置长度为N的信号X在正交基Ψ上是K-稀疏(即含有k非零值)；

(2)如果能找到一个和Ψ观测基础不相关(不相关)Φ;

(3)使用观测基Φ观察原始信号以获得长度M一维测量值M个观测值Y，K

(4)然后可以用各种优化 *** 从观测值中使用Y高概率恢复X。

压缩感知高概率重构信号的过程如下图2所示：

图2

数学表达

压缩感知方程为：y=Φx=ΦΨs=Θs。(图3)

其中设x为长度为N稀疏度为一维信号k(即含有k非零值)，y为长度为M一维测量值，Φ观察矩阵，Ψ为稀疏基，s稀疏系数。

然后将原来的测量矩阵进行测量Φ变换为Θ=ΦΨ，解出s的逼近值s’，则原信号x’ = Ψs’。

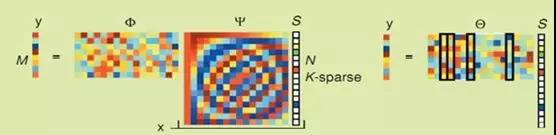
图3

压缩感知获取和解决 ***

应用压缩感知有两个主要问题：

问题1：如何设计稀疏的观测矩阵和信号基，以获得更好的观测值，解决方案如下表1：

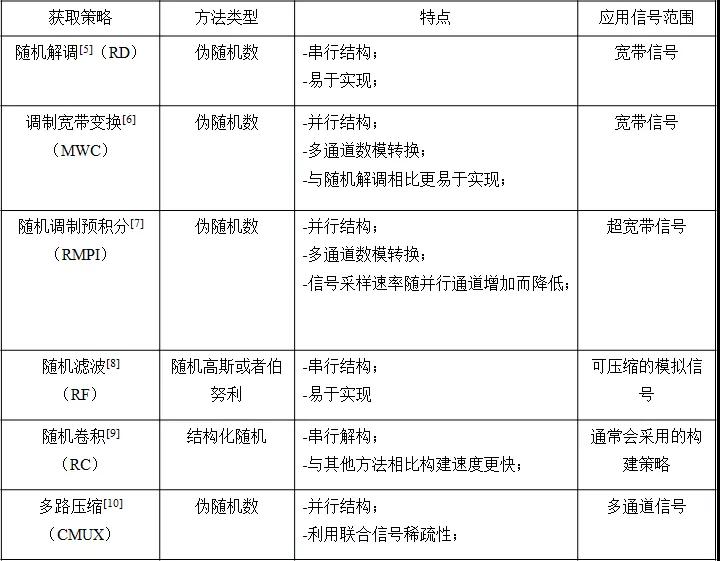
表1

问题2：如何有效地重构信号，即在压缩感知方程中找到信号x近似解。求解 *** 如下图4所示：

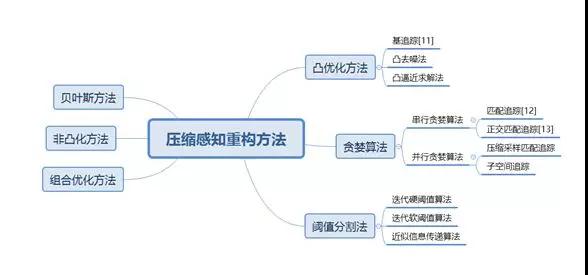
图4 压缩感知信号重构 ***

三.压缩感知的应用领域和应用实例

压缩传感技术是压缩感知理论的应用之一。它是一个抽象的数学概念，最初用于图像处理，并逐渐扩展到成像以外的许多领域。

说到压缩感知的成功应用，首当其冲的是美国Rice大学发明的单像素相机[14]。在整个系统中，被拍摄对象的图像被镜头击中DMD(数字微镜芯片，Digital Micromirror Device)上，而经过DMD反射图像通过二次镜头聚焦在只有一个像素的传感器上，形成光信号。在拍摄过程中，DMD每个镜头反射的明暗矩阵以伪随机代码的形式快速变换，每个变化形成一个像素信号。通过综合计算每个信号和伪随机代码，得到对象的图像。相机的模型和结构如下图5所示：

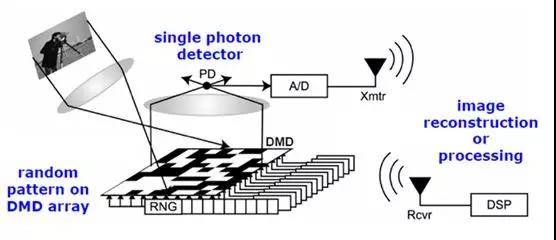
图5

该相机的关键部件是由德州仪器生产的数字微镜芯片(DMD)，这款芯片主要用在数字背投或是投影机中。DMD它由大量只有细菌大小的镜片组成，每个微镜片一侧反射而不反射，可以快速翻转。

以下是几个应用:

               
• 图像信息安全。压缩感知具有采样、压缩和加密数据的良好特性，在图像安全方面引起了研究人员的广泛关注。目前，整合压缩感知，学者将其应用于图像加密、图像哈希、数据隐藏和安全图像检索技术。例如，提出了一些基于压缩感知的水印 *** ，它们可以用信道的数据传输和隐藏有用信息。
               
• 无线传感器 *** (WSN)。由于传感器节点收集的数据具有时间和空间相关性，信号稀疏可压缩，传感器节点资源有限，聚合节点性能强，适用于压缩感知理论编码简单、解码复杂的特点，因此基于压缩感知 WSN 数据收集技术已逐步深入和广泛地研究和发展。Bajwa和Haupt将压缩感知理论应用于无线传感器 *** 的数据采集[15]。
               
• 磁共振成像(MRI)。在医学上，磁共振的工作原理是多次测量(但次数仍然有限)(基本上是离散拉东人体图像的转换—或称为X光转换），然后处理数据以生成图像。由于测量次数必须很多，整个过程对患者来说太长了。压缩传感技术可以显著减少测量次数，加速成像（甚至可能实现实时成像，即核磁共振视频而不是静态图像）。此外，我们还可以测量图像质量的数量，即使用相同的测量次数可以获得更高的图像分辨率。
               
• 线性安全编码。压缩传感技术提供了一种简单的 *** ，允许多个传输者将其信号带纠错并传输，以便即使输出信号的大部分丢失或损坏，原始信号仍然可以恢复。例如，1000比特信息可以用任何线性编码编码到3000比特流。然后，即使其中300人被（恶意）损坏，原始信息也可以完全重建，没有损失。这是因为压缩传感技术可以将损坏动作本身视为稀疏信号（仅集中在3000比特中的300）。

四.总结与展望

随着压缩感知理论及其技术的发展，信号处理的许多领域发生了革命性的变化，人们将其应用于许多信号处理领域，如视频目标跟踪[16]、无线传感器 *** 数据安全传输和采集[17]、图像加密算法[18]等，这些技术也可用于信息安全。压缩感知已成为信号处理领域的武器。由于严格的数学证据和推导，压缩感知具有相对较深的理论基础。压缩感知的信号采集和重建算法因信号而异，因此拥有一个通用的压缩感知信号采集和重建策略将非常有益，这也将是所有研究人员的目标。

参考文献：

[1] E. J. Candès,Tao T . Near-Optimal Signal Recovery From Random Projections: Universal Encoding Strategies?[J]. IEEE Transactions on Information Theory,2006,52(12):5406-5425.

[2] Donoho D L . Compressed sensing[J]. IEEE Transactions on Information Theory,2006,52(4):1289-1306.

[3] E. J. Candès,Emmanuel & Romberg,Justin & Tao,Terence. Robust Uncertainty Principles:Exact Signal Frequency Information. [J] IEEE Transactions on Information Theory,2006,52:489-509.

[4] E. J. Candès and M. B. Wakin,‘An introduction to compressive sampling’ IEEE Signal Process. Mag.,vol. 25,no. 2,pp. 21–30,Mar. 2008.

[5] Laska J N ,Kirolos S ,Duarte M F ,et al. Theory and Implementation of an Analog-to-Information Converter using Random Demodulation[C]// IEEE International Symposium on Circuits & Systems. IEEE,1962.

[6] Mishali M ,Eldar Y C . From Theory to Practice: Sub-Nyquist Sampling of Sparse Wideband Analog Signals[J]. IEEE Journal of Selected Topics in Signal Processing,2010,4(2):375-391.

[7] Yoo J ,Becker S ,Monge M ,et al. Design and implementation of a fully integrated compressed-sensing signal acquisition system[C]// Acoustics,Speech and Signal Processing (ICASSP),2012 IEEE International Conference on. IEEE, 2012.

[8] Tropp J A . Random Filters for Compressive Sampling[C]// Conference on Information Sciences & Systems. IEEE,2006.

[9] Romberg,Justin. Compressive Sensing by Random Convolution[J]. SIAM Journal on Imaging Sciences,2009,2(4):1098-1128.

[10] Slavinsky J P ,Laska J N ,Davenport M A ,et al. The compressive multiplexer for multi-channel compressive sensing[C]// IEEE International Conference on Acoustics. IEEE,2011.

[11] Chen S S ,Saunders D M A . Atomic Decomposition by Basis Pursuit[J]. SIAM Review,2001,43(1):129-159.

[12] S. G. Mallat and Z. Zhang,Matching pursuits with time-frequency dictionaries,[J]IEEE Trans. Signal Process,1993.

[13] Y. C. Pati,R. Rezaiifar,and P. S. Krishnaprasad,Orthogonal matching pursuit: Recursive function approximation with applications to wavelet decomposition,[C] in Proc. 27th Asilomar Conf. Signals,Syst. Comput.,vol. 1. Pacific Grove,CA,USA,1993,pp. 40–44.

[14] Duarte M F ,Davenport M A ,Takhar D ,et al. Single-Pixel Imaging via Compressive Sampling[J]. IEEE Signal Processing Magazine,2008,25(2):83-91.

[15] Bajwa W U Z ,Haupt J ,Sayeed A M ,et al. Compressive wireless sensing[C]// Proceedings of the Fifth International Conference on Information Processing in Sensor Networks,IPSN 2006,Nashville,Tennessee,USA,April 19-21,2006. ACM,2006.

[16] Liu J,Han C,Han F. A novel compressed sensing based track before detect algorithm for tracking multiple targets.[C]// International Conference on Information Fusion. 2013.

[17] 包明杰、张浩然、公主. 无线传感 *** 应用压缩感知综述[J]. 2016年35日(14)微型机及应用:16-18.

[18] 王海娇.研究了基于压缩感知的图像加密和检索 *** [D].

【本文为51CTO专栏作者“中国保密协会科技分会”请联系原作者转载原稿

戳这里，看作者更好的文章